Cargando...
Recursos educativos
-
Nivel educativo
-
Competencias
-
Tipología
-
Idioma
-
Tipo de medio
-
Tipo de actividad
-
Destinatarios
-
Tipo de audiencia
-
Creador
Lo más buscado
- Repaso de tiempos verbales en inglés
- Ser y estar
- Aprender a reciclar
- Repaso de fisica
- Descargar ejercicios de ingles
- Letras S
- Conocimiento del medio natural, social y cultural
- Ejercicios de signos de interrogación
- colorear dibujo
- Repaso y material didáctico adicional
- Aprender a escribir
- Problemas de división
- Generador de anagramas
- método lectoescritura
- Guía interactiva de minerales
-

Combinatoria: binomio de Newton
estudiia Organización
- 2 lo usan
- 5953 visitas
Explicamos cómo se aplica la fórmula del Binomio de Newton para el cálculo de potencias de binomios. Y realizamos un ejemplo.
-
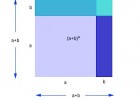
Cuadrado de un binomio
Tiching explorer Organización
- 2 lo usan
- 7370 visitas
Recurso basado en un applet para la visualización gráfica del cuadrado de un binomio.
-

Binomio de Newton - Vitutor
mayk paredes guevara Docente
- 1 lo usan
- 2346 visitas
El binomio de Newton, fórmula, cálculo del término que ocupa el lugar k, teoría del binomio de Newtonm ejemplos prácticos, ejercicios resueltos.
-

Polinomio entre Binomio
EducaMadrid Organización
- 1 lo usan
- 5674 visitas
Vídeo para trabajar el cociente de polinomios: polinomio entre binomio.
-

Potencia de un binomio
EduBook Organización
- 2 lo usan
- 1630 visitas
Polinomios y fracciones algebraicas
-

El Binomio Algebraico.pdf
LUIS CARLOS LASPRILLA TOVAR Docente
- 1 lo usan
- 1509 visitas
-

El binomio de Newton
Xtec Organización
- 1638 visitas
Webquesta que té com a principal objectiu que l'alumnat aprengui a fer servir fòrmules que li permeti conèixer de forma ràpida i eficaç el cub, les potències quarta, cinquena, etc d'un…
-

El Binomio Algebraico.pdf
LUIS CARLOS LASPRILLA TOVAR Docente
- 1 lo usan
- 1215 visitas
-

El Binomio Algebraico.pdf
LUIS CARLOS LASPRILLA TOVAR Docente
- 1397 visitas
-

Binomio de Newton
Cristina Seco Organización
- 1082 visitas
Pàgina web en la que se deduce la fórmula que nos permitirá elevar a cualquier potencia de exponente natural, n, de un binomio.
Te estamos redirigiendo a la ficha del libro...







